Персональный сайт - решение ГИА

Текст задания.

Исполнитель Робот умеет перемещаться по лабиринту, начерченному на плоскости, разбитой на клетки. Между соседними (по сторонам) клетками может стоять стена, через которую Робот пройти не может.
У Робота есть восемь команд. Четыре команды – это команды-приказы: вверх, вниз, влево, вправо
При выполнении любой из этих команд Робот перемещается на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →. Если Робот получит команду передвижения через стену, то он разрушится.
Ещё четыре команды – это команды проверки условий. Эти команды проверяют, свободен ли путь для Робота в каждом из четырёх возможных направлений: сверху свободно, снизу свободно, слева свободно, справа свободно.
Также у Робота есть команда закрасить, при которой закрашивается клетка, в которой Робот находится в настоящий момент.

Выполните задание.

На бесконечном поле имеется лестница. Сначала лестница спускается вниз справа налево, затем спускается вниз слева направо. Высота каждой ступени – одна клетка, ширина – две клетки. Робот находится справа от верхней ступени лестницы.
Количество ступенек, ведущих влево, и количество ступенек, ведущих вправо, неизвестно. На рисунке указан один из возможных способов расположения лестницы и Робота (Робот обозначен буквой «Р»).
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные непосредственно над ступенями лестницы, спускающейся слева направо. Требуется закрасить только клетки, удовлетворяющие данному условию.
Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля. При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться

Решение:
В данном задании необходимо составить алгоритм для Робота по условию задачи. Для составления алгоритма рассмотрим поле по условию задания для Робота, на котором находится лестница. Роботу необходимо пройти по лестнице сначала спускаясь справа налево, затем слева направо закрашивая клетки. Нам необходимо учитывать, что количество ступенек неограниченно, значит для прохождения ступенек используется цикл с определенным условием и системой команд.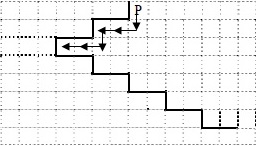

Рассмотрим первый рисунок, на котором мы видим начальное положение Робота и систему повторяющихся команд: вниз, влево, влево, а условием для цикла является свободная клетка внизу (в данном случае нужно правильно определить условие цикла, т.к. Робот идет вниз, то в
первую очередь проверка свободной клетки внизу).

После выполнения данного цикла Робот встанет на стыке лестниц. Рассмотрим второй рисунок. Далее необходимо организовать цикл с системой повторяющихся команд внутри: закрасить, вправо, закрасить, вправо, вниз и условием проверки на свободное прохождение вправо, т.е. справа свободно (в данном случае первоначальные шаги делаются вправо и число клеток ступеньки и число клеток вниз нам известно).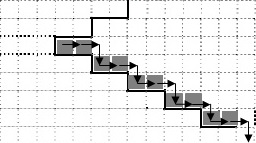

Данный цикл будет работать до конца лестницы, но при окончании лестницы цикл тоже может работать если справа будет свободно (по второму рисунку можно заметить), т.е. поле не закончилось. Но по условию задания Робот должен закрасить клетки только над ступенями. Поэтому в цикл необходимо внести условие "если" с проверкой стены, т.к. в конце лестницы стен нет,
например: если слева стена, то
или если снизу стена, то
Т.е. данное условие помогает Роботу ориентироваться на поле и не дает выполнять лишних действий.

Теперь нам видно, что алгоритм для Робота будет состоять из двух циклов.

алгоритм
нач.
пока снизу свободно, выполнить
нц
вниз
влево
влево
кц
пока справа свободно, выполнить
нц
если снизу стена, то
нв
закрасить
вправо
закрасить
вправо
вниз
кв
кц
кон.

вернуться

Сайт учителя Фадеева А.В.

решение ГИА - 20.1